Tutorial 2

Linear Algebra I: Vectors

[insert your name]

Important reminders: Before starting, click “File -> Save a copy in Drive”. Produce a pdf for submission by “File -> Print” and then choose “Save to PDF”.

To complete this tutorial, you should have watched Video 1.1: Vectors, Video 1.2: Vector operations, and Video 1.3: Vector spaces.

# Imports
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import ipywidgets as widgets   

# Plotting parameters
matplotlib.rcParams.update({'font.size': 22})

Exercise 1: Figuring out a basis

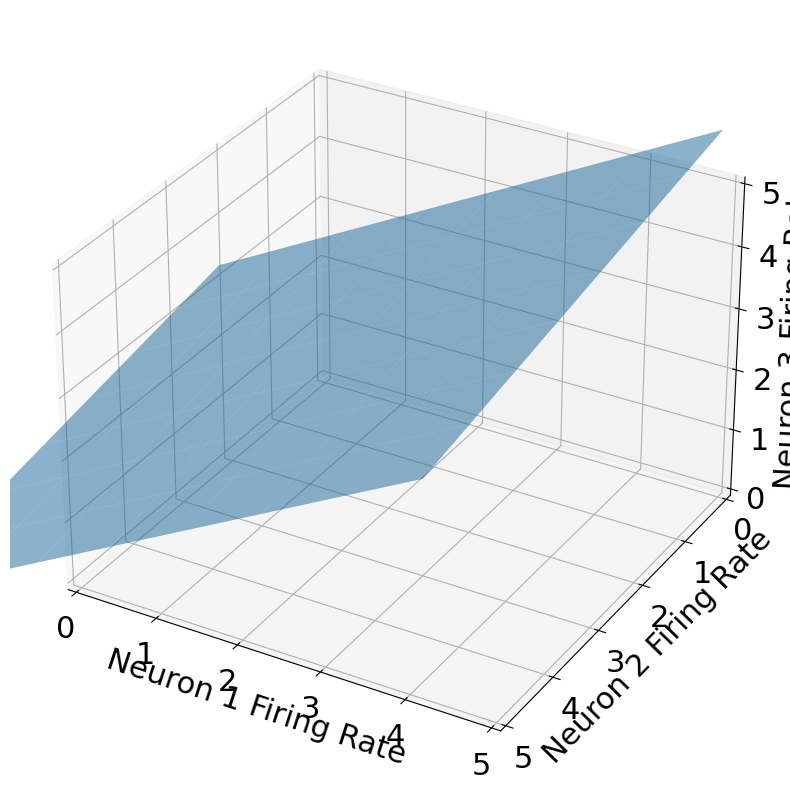
Let’s say we are looking at the firing rates of 3 neurons. We can represent their activity in a 3D plot, as below. It turns out that due to their tightly-linked interactions, they always fire in such a way that the point in 3D space falls along a 2D plane (that passes through the origin). Basically, every single data point we record of the firing rates of the 3 neurons falls on that plane. This is represented by the blue plane in the figure below. This 2D plane is a subspace of all of 3-D space (R3).

A) How many basis vectors would you need for the 2D plane? How many components would each basic vector have?

B) How many numbers would you need to be able to fully describe the state of the 3 neuron population at a given time?

YOUR ANSWER HERE

Execute this cell to see figure

# @markdown Execute this cell to see figure

fig = plt.figure(figsize = (10, 10))

# add axes
ax = fig.add_subplot(111,projection='3d')

xx, yy = np.meshgrid(range(-4, 4), range(-4, 4))
z = .7*xx + -.2*yy

# plot the plane
ax.plot_surface(xx, yy, z, alpha=0.5)

ax.set(xlim = [0, 5], ylim = [5, 0], zlim = [0, 5], xlabel = 'Neuron 1 Firing Rate',  ylabel = 'Neuron 2 Firing Rate', zlabel = 'Neuron 3 Firing Rate');
#ax.invert_xaxis()

Exercise 2: Determing dependence

Let’s say we have four vectors:

\[\begin{split} \mathbf{a} = \begin{bmatrix} 4 \\ 2 \\ 0 \end{bmatrix}, \mathbf{b} = \begin{bmatrix} 1 \\ 0 \\ 3, \end{bmatrix}, \mathbf{c} = \begin{bmatrix} 5 \\ 2 \\ 3 \end{bmatrix}, \mathbf{d} = \begin{bmatrix} 3 \\ 3 \\ 2 \end{bmatrix}\end{split}\]

Check out this visualization prepared by Oğul Can Yurdakul to better see the vectors: https://www.geogebra.org/3d/hherq78z!

1. Are these vectors linearly independent or dependent? Why?

2. What is the span of the set of vectors \(\{\mathbf{a}, \mathbf{b}, \mathbf{c}, \mathbf{d}\}\)?

3. What is the span of the set of vectors \(\{\mathbf{a}, \mathbf{b}, \mathbf{c}\}\)?

4. What is the span of a set just consisting of vector \(\{\mathbf{a}\)} (in general terms)?

5. What is the span of the set of vectors \(\{\mathbf{a}, \mathbf{b}\)} (in general terms)?

A) Linear independence vs dependence

Are these vectors linearly independent or dependent? Why?

Your text answer here

B) Orthogonal vectors

Are vectors \(\bar{a}\) and \(\bar{b}\) orthogonal? How do you know?

Your text answer here

C) Span

i) What is \(Span\{\bar{a}, \bar{b}, \bar{c}, \bar{d}\}\)?

ii) What is \(Span\{\bar{a}, \bar{b}, \bar{c}\}\)?

iii) What is \(Span\{\bar{a}\}\)?

Your text/math answer here

D) Basis

Can you make a basis for \(R^3\) based on the above vectors? What is it?

Your text answer here

(Optional, advanced) Exercise 3: Vector Projections

We want to find the projection of one vector onto another, by which we essentially mean the component of a vector that lies along another vector. For two vectors \(\bar{a}\) and \(\bar{b}\), can you come up with the formula (and proof of that formula) for the projection of \(\bar{b}\) onto \(\bar{a}\) (the green vector below)?