Key Concepts
Contents
Key Concepts#
Differential equations#
Equations that relate functions and their derivatives (\(\frac{dx}{dt} = F(x, t)\))
Can sometimes compute the analytical solution \(x(t)\) by integration and solving for constants using the initial condition. This is not always possible.
Can numerically approximate specific trajectories (corresponding to different initial conditions) using Euler’s method, which is based on the update rule $\( x(t+\Delta t) = F(x, t)\Delta t + x(t)\)$
Can understand the system graphically by plotting a direction field (tangent lines on x vs t graph)
Can also understand the system graphically by plotting \(\frac{dx}{dt}\) vs x and analyzing critical/equilibrium points
Critical/equilbrium points occur at x for which \(\frac{dx}{dt} = 0\). They are either stable (attractors) or unstable (repellers) depening on the derivative sign to either side
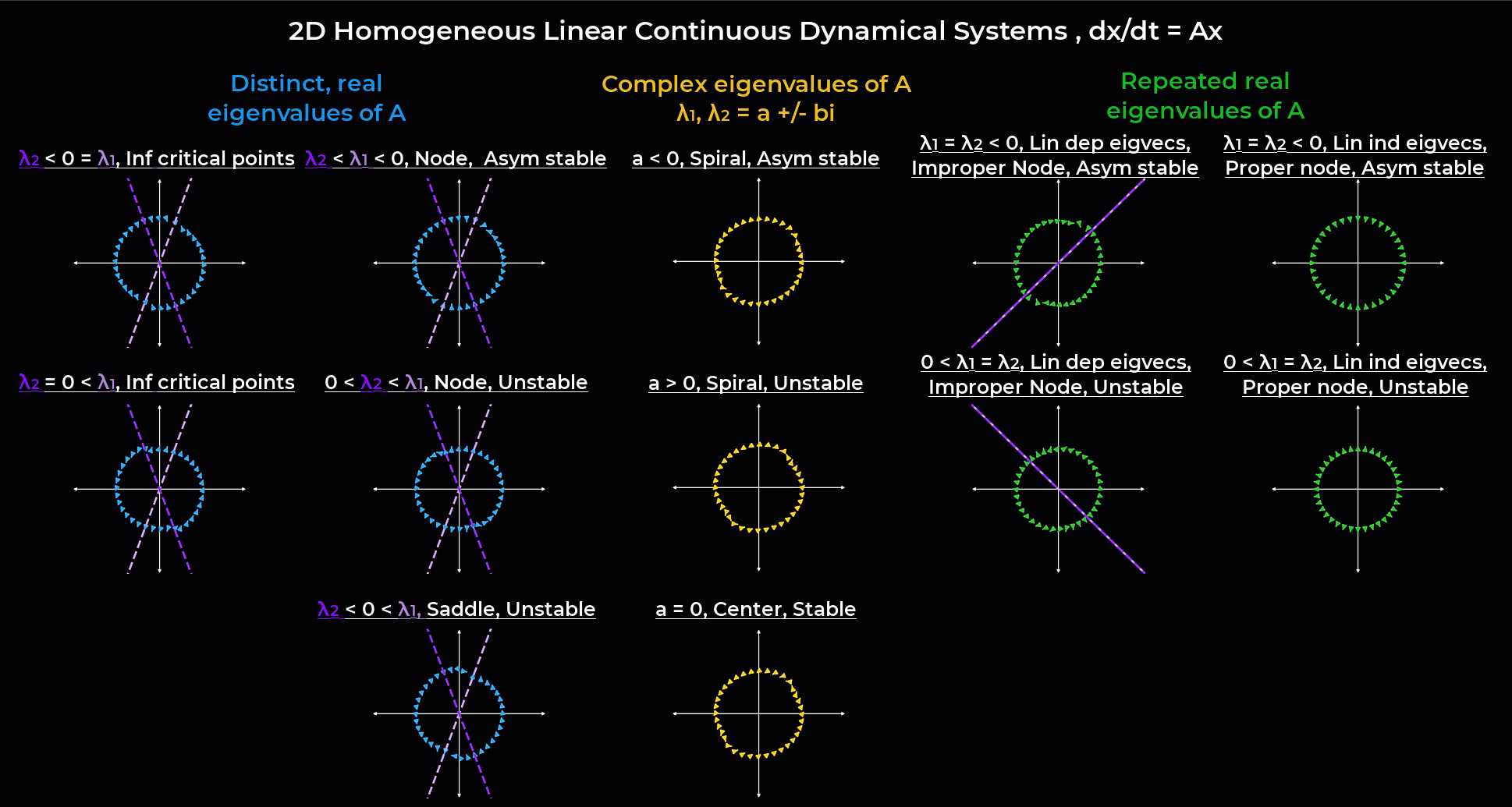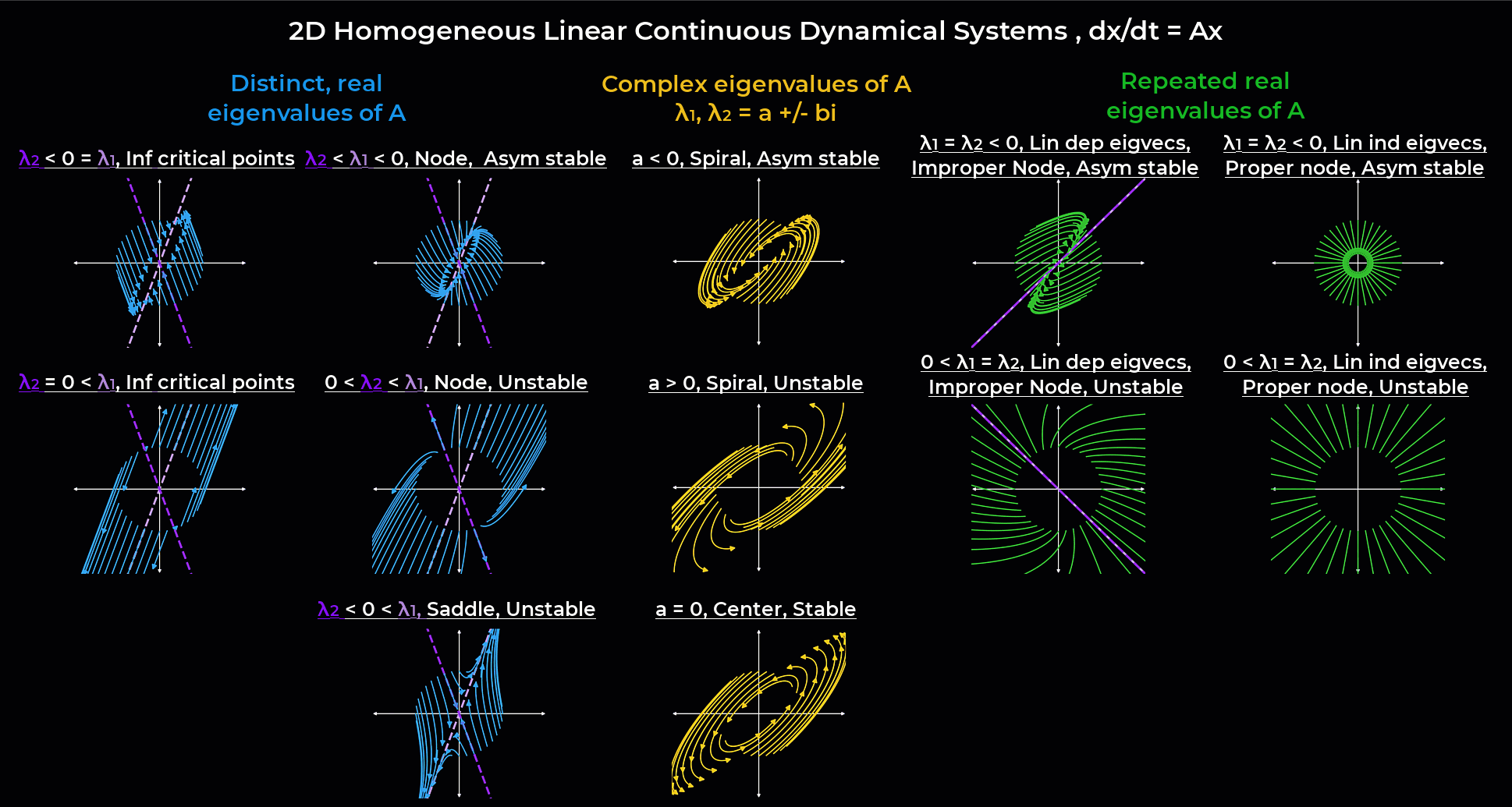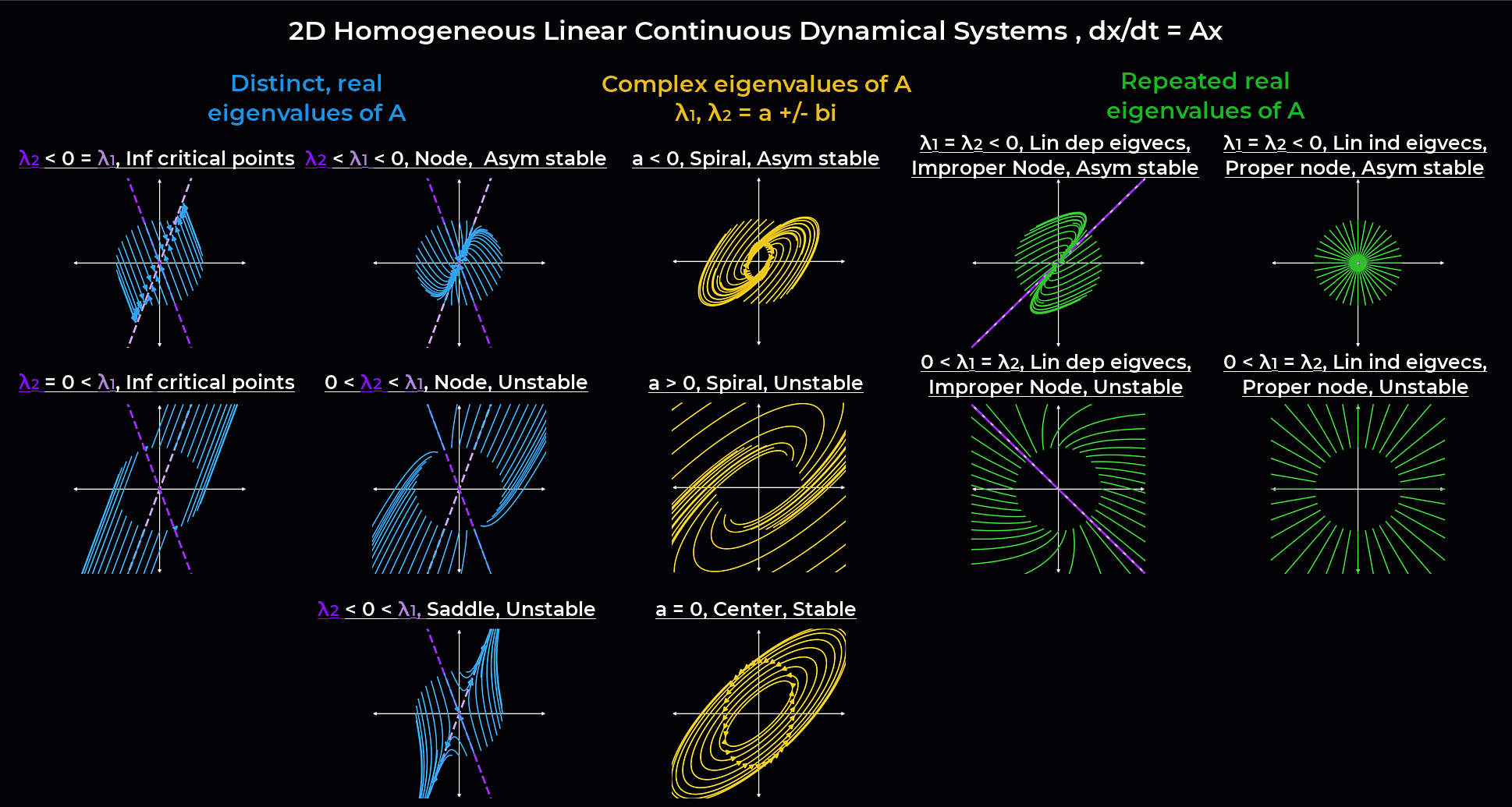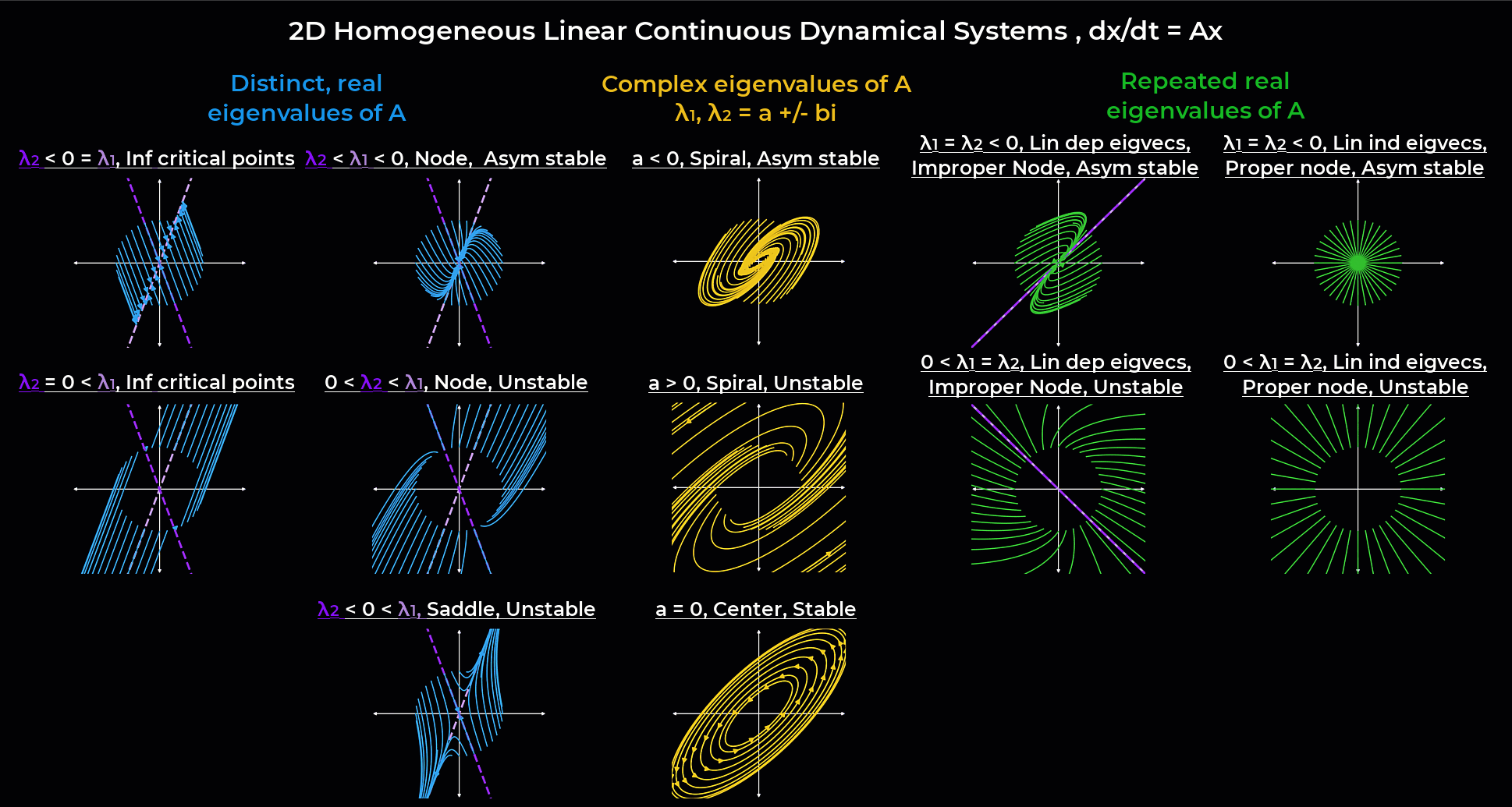
Systems of differential equations#