Key concepts

Model evaluation

• Model evaluation: is our fitted model any good?

• If the model is too simple to capture the data, we will underfit the data. We will have high bias and low variance and bad performance on both training and test data.

• If the model is too complex, we will overfit to the noise of the data. We will have high variance, low bias, good performance on training data, and bad performance on test data.

• In machine learning, we usually evaluate on held-out test data (data not used for fitting the model). We should not touch the test data until we are ready to evaluate the model (for example, the test data shouldn’t be used for any preprocessing steps)

• A more statistics-based approach for model evaluation is to ask how confident we are in the model parameters/predictions. We can use confidence intervals for this as these explicitly report uncertainty. We use bootstrapping to construct our confidence intervals since we cannot access the actual distribution of the data.

• In bootstrapping, we resample from our data with replacement, fit the model again to each resampling, and collect the estimates for a parameter into a distribution. We can then estimate the confidence intervals as the middle 95% of the bootstrapped estimates.

Model selection

• Model selection: which model should we choose?

• We cannot compare models on test data.

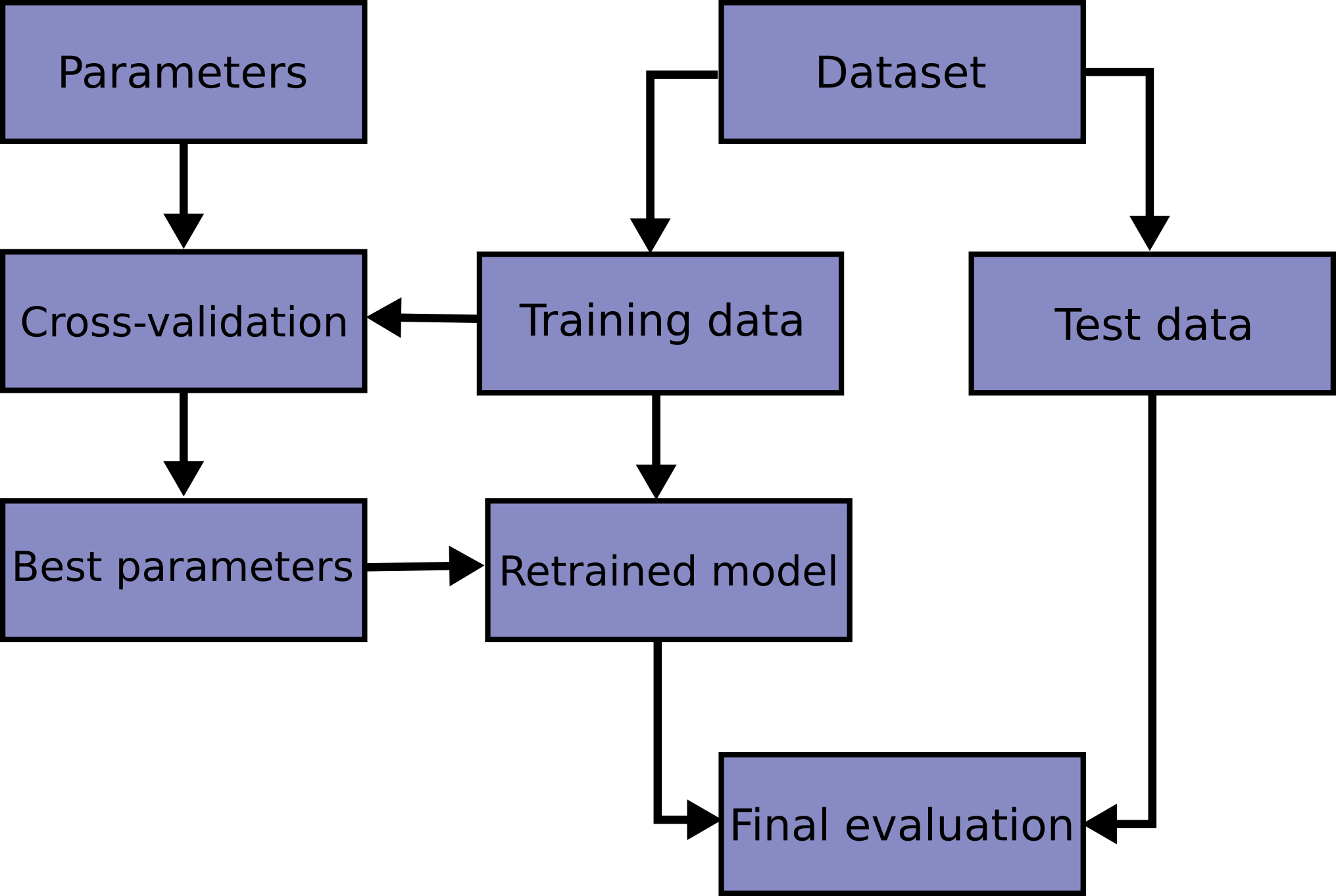
• Cross-validation: create a third data partition: validation data. Fit all models on training data, select the model with best validation performance, and then evaluate the chosen model on test data.

• k-fold cross-validation: if we don’t want to permanently lose some data by assigning it as validation data, we can use k-fold cross-validation. See the two figures below to summarize this procedure (from sklearn website)

• We can also use model selection methods that ask how likely the data is under a given model. Akaike’s Information Criterion is one such method that balances model complexity with goodness of fit. For each model, we compute \(AIC = 2K - 2 log L\) where K is the number of parameters and L is the likelihood of the data given the model. We then select the model with smallest AIC.